Quiz 12-1 introduction to trig the unit circle – Quiz 12-1: Introduction to Trigonometry and the Unit Circle delves into the fundamental concepts of trigonometry, establishing a solid foundation for understanding the intricate relationship between angles and the unit circle. This exploration unravels the mysteries of radians and degrees, delving into the definitions of sine, cosine, and tangent functions, and uncovering their captivating graphs.
Through engaging examples and real-world applications, this quiz illuminates the practical significance of trigonometry in various fields, solidifying its importance as a cornerstone of mathematical knowledge.
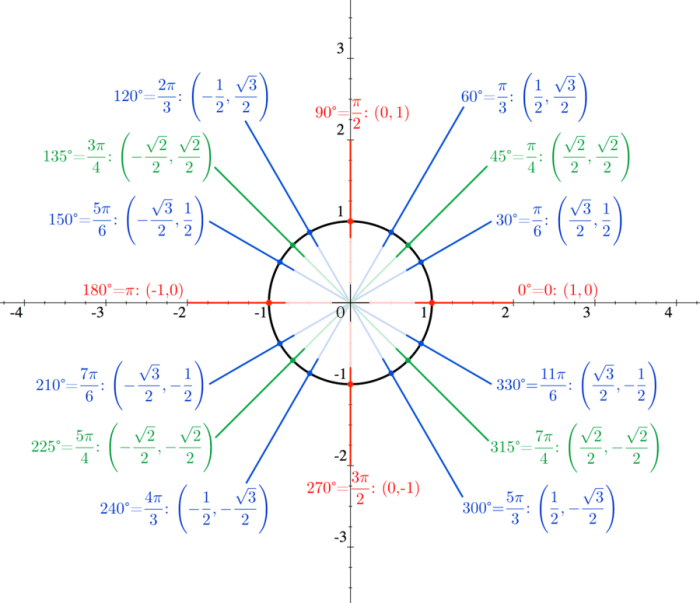
Introduction to the Unit Circle

The unit circle is a circle with a radius of 1. It is often used in trigonometry to represent the values of the sine and cosine functions.
The unit circle can be drawn in the coordinate plane with the center at the origin. The positive x-axis is the horizontal diameter of the circle, and the positive y-axis is the vertical diameter of the circle.
The unit circle is divided into four quadrants. The first quadrant is the quadrant in which both the x-coordinate and the y-coordinate are positive. The second quadrant is the quadrant in which the x-coordinate is negative and the y-coordinate is positive.
The third quadrant is the quadrant in which both the x-coordinate and the y-coordinate are negative. The fourth quadrant is the quadrant in which the x-coordinate is positive and the y-coordinate is negative.
Radians and Degrees
Radians and degrees are two different units of measure for angles. A radian is the measure of an angle that intercepts an arc of length 1 on a circle with radius 1. A degree is the measure of an angle that intercepts an arc of length 1/360 on a circle with radius 1.
There are 2π radians in a full circle, and there are 360 degrees in a full circle.
To convert from radians to degrees, multiply the angle in radians by 180/π. To convert from degrees to radians, multiply the angle in degrees by π/180.
Sine and Cosine Functions, Quiz 12-1 introduction to trig the unit circle
The sine function and the cosine function are two of the most important functions in trigonometry. The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle.
The cosine function is defined as the ratio of the length of the adjacent side to the length of the hypotenuse of a right triangle.
The sine function and the cosine function can be graphed using the unit circle. The sine function is graphed as the y-coordinate of the point on the unit circle that corresponds to the angle. The cosine function is graphed as the x-coordinate of the point on the unit circle that corresponds to the angle.
Tangent Function
The tangent function is defined as the ratio of the length of the opposite side to the length of the adjacent side of a right triangle. The tangent function can be graphed using the unit circle. The tangent function is graphed as the slope of the line that passes through the origin and the point on the unit circle that corresponds to the angle.
Applications of Trigonometry
Trigonometry is used in a wide variety of applications, including engineering, physics, and navigation. In engineering, trigonometry is used to calculate the forces and stresses on structures. In physics, trigonometry is used to calculate the motion of objects. In navigation, trigonometry is used to calculate the distance and direction to a destination.
Popular Questions: Quiz 12-1 Introduction To Trig The Unit Circle
What is the unit circle?
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane.
How are radians and degrees related?
1 radian is equal to 180/π degrees.
What is the sine function?
The sine function is a trigonometric function that gives the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle.